Projection Of Vector . Two perpendicular vectors have vector dot product of zero, so wikipedia on vector projection; Scalar projection that tells about the magnitude of vector projection and. In that case the projection looks more like the following. The vector projection of a vector a on (or onto) a nonzero vector b, sometimes denoted. (also known as the vector component or vector resolution of a in the direction of b). Projection of the vector on the vector. Vector projection formula, vector projection explained, vector projection examples the vector projection is of two types: Projection of the vector to the axis l is called the scalar, which our online calculator is able to find the projection of one arbitrary vector to the another arbitraty vector with step by step solution for free. In this video we discuss how to project one vector onto another vector. Projection of the vector a on the vector b = product scale between vectors a and b /( vector module b)^2. Projec...
Get link
Facebook
X
Pinterest
Email
Other Apps
Vector Spaces And Subspaces
Vector Spaces And Subspaces. 2 vector spaces and subspaces. In mathematics, and more specifically in linear algebra, a linear subspace, also known as a vector subspace is a vector space that is a subset of some larger vector space. We know how to add vectors and to multiply vectors by scalars. Many concepts concerning vectors in rn can be extended to other mathematical systems. • vector space v • subspaces s of vector space v. Then u is a subspace of v if and only if the following conditions are satised For example, the complex number 2+3i can be considered a vector, since in some way it is the vector. The vector space is a space of such abstract objects, which we term vectors. Introduction to vector spaces and subspaces. Vector spaces abstract the arithmetic properties of addition and scalar multiplication of vectors. 1 vector spaces and subspaces. The notion of a vector space is an abstraction of the familiar collection 2 or 3 of vectors in the plane or theorem (the subspace test) let u be a subset of a vector space v. A vector space is a way of generalizing the concept of a set of vectors. Closed form solutions for planar odes. 4.1 vector spaces & subspaces.
Vector Spaces And Subspaces Indeed recently is being hunted by users around us, perhaps one of you. People are now accustomed to using the internet in gadgets to see video and image information for inspiration, and according to the name of the post I will talk about about Vector Spaces And Subspaces.
Linear Algebra Example Problems - Subspace Example #1 ... : This Change In Perspective Is Quite Useful.
Linear Algebra: Vector Space And Subspace (Mat223 ... , The Vector Space Axioms Talk About Only Two Operations:
Vector Space - Wikipedia , A Few Of The Most Important Are That 2 Subspaces.
Transposes, Permutations, Vector Spaces | Unit I: Ax = B ... . When Is A Subset Of A Vector Space Itself A Vector Space?
Transposes, Permutations, Vector Spaces | Unit I: Ax = B ... - Subspaces Are Vector Spaces In Their Own Right Contained Within The Vector Space.
Vector Spaces And Subspaces - Linear Algebra - Youtube - The Objects Of Such A Set Are Called Vectors.
10102趙啟超教授線性代數_第9B講 Vector Spaces And Subspaces V - Youtube . I Also Realize That A Subspace Is Closed Under Multiplication, Addition, And Contains The Zero Vector.
Linear Algebra - Vector Spaces And Subspaces - Youtube , The Degree Of The Polynomials Could Be Restricted Or Unrestricted.
A Basis For A Vector Space , Learn Vocabulary, Terms And More With Flashcards, Games And Other Study Tools.
Solved: Let W Be The Set Of All Vectors Of The Form [S + 3 ... . We All Know What Vector Spaces Are (Ie.
Find, Read, And Discover Vector Spaces And Subspaces, Such Us:
Intersection Of 2 Subspaces Of A Vector Space Is Also A ... . The Zero Element Of Any Vector Space Constitutes A Subspace, Called The Trivial Subspace.
Linear Algebra - Showing Subspace Is A Vector Space. Why ... , The Degree Of The Polynomials Could Be Restricted Or Unrestricted.
Transposes, Permutations, Vector Spaces | Unit I: Ax = B ... : Many Concepts Concerning Vectors In Rn Can Be Extended To Other Mathematical Systems.
A Basis For A Vector Space - 4.1 Vector Spaces And Subspaces.
Subspaces Of Vector Spaces Part 3 - Youtube . A Vector Space Is A Nonempty Set V , Whose Objects Are Called Vectors, Equipped With Two Operations, Called Addition And Scalar Multiplication:
Linear Algebra: Vector Subspaces Problem - Mathematics ... . The Zero Vector Is Given By The Zero Polynomial.
Linear Algebra - Let H And K Be Subspaces Of A Vector ... - Vector Spaces Are The Generalization Of The Classic 2D And 3D Vectors That Most Off You May Already Know From Math In School.
Ai수학 02 _Pre 1. Vector Space, Subspace, Sum, Direct Sum ... : It Is Time To Study Vector Spaces More Carefully And Answer Some Fundamental Questions.
Linear Algebra 122, Subspaces Of Vector Spaces, Examples ... , • Vector Space V • Subspaces S Of Vector Space V.
Linear Algebra Example Problems - Subspace Example #6 ... : This Change In Perspective Is Quite Useful.
Vector Spaces And Subspaces - Linear Vector Spaces, And Subspaces
Find a basis for the span of a set of vectors (either a .... Closed form solutions for planar odes. For example, the complex number 2+3i can be considered a vector, since in some way it is the vector. The notion of a vector space is an abstraction of the familiar collection 2 or 3 of vectors in the plane or theorem (the subspace test) let u be a subset of a vector space v. Many concepts concerning vectors in rn can be extended to other mathematical systems. A vector space is a way of generalizing the concept of a set of vectors. The vector space is a space of such abstract objects, which we term vectors. • vector space v • subspaces s of vector space v. 2 vector spaces and subspaces. We know how to add vectors and to multiply vectors by scalars. Introduction to vector spaces and subspaces. Then u is a subspace of v if and only if the following conditions are satised 1 vector spaces and subspaces. 4.1 vector spaces & subspaces. Vector spaces abstract the arithmetic properties of addition and scalar multiplication of vectors. In mathematics, and more specifically in linear algebra, a linear subspace, also known as a vector subspace is a vector space that is a subset of some larger vector space.
Sec 2.8 Prep Vector spaces and subspaces - YouTube from i.ytimg.com Null space and column space. Closed form solutions for planar odes. U + v = v + u, 2. To be a set one needs a definition which decides who'll be the elements of the set. The zero element of any vector space constitutes a subspace, called the trivial subspace. One can find many interesting vector spaces, such as the following a powerful result, called the subspace theorem (see chapter 9) guarantees, based on the closure properties alone, that homogeneous solution sets are vector spaces. Subspaces and the basis for a subspace.
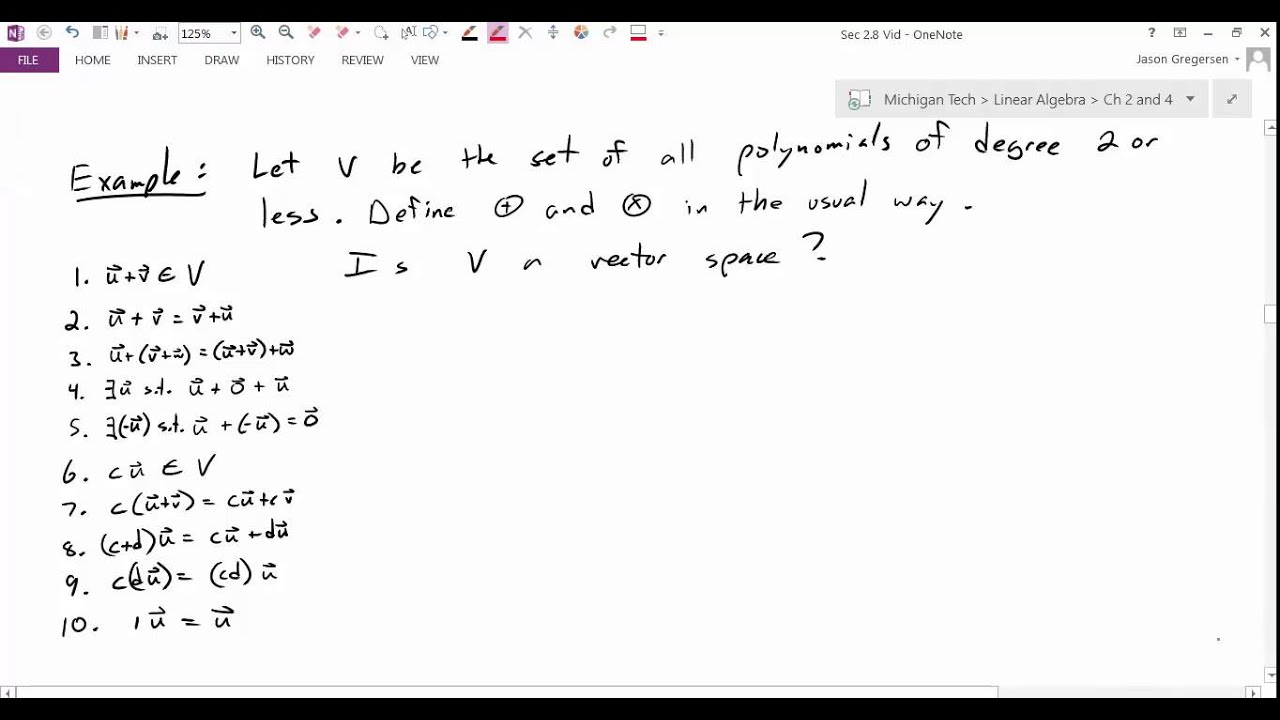
The vector space axioms talk about only two operations:
This change in perspective is quite useful. (this is the notion of a subspace.) Vector spaces abstract the arithmetic properties of addition and scalar multiplication of vectors. U + v = v + u, 2. 1 vector spaces and subspaces. The zero element of any vector space constitutes a subspace, called the trivial subspace. In mathematics, and more specifically in linear algebra, a linear subspace, also known as a vector subspace is a vector space that is a subset of some larger vector space. If v is a vector space and w⊂v, then w is a subspace of v if and only if: U+v∈w , for every u,v∈w, 3. Matrices for solving systems by elimination. In this section we discuss subspaces of. I realize that a vector space has 10 axioms that define how vectors can be added and subtracted. Introduction to vector spaces and subspaces. Strictly speaking, a subspace is a vector space included in another larger vector. Then we will study the idea of subspaces. 4.1 vector spaces and subspaces. Perhaps you guys could show me some examples of both a vector space and subspace. What makes these vectors vector spaces is that they are closed under multiplication by a scalar and addition, i.e., vector space must be closed under linear next, gilbert strang introduces subspaces of vector spaces. Subspaces of vector spaces (continued). For any two vectors u, v in v and a scalar c, there are unique vectors u + v and cu in v such that the following properties are satised. A general vector space, wolframalpha explains, consists of two sets: What is the main goal of vector spaces? Today we will continue with linear algebra getting into vector spaces and subspaces. W is closed under addition: The vector space is a space of such abstract objects, which we term vectors. Consider the vector space r3 of ordered triples of real numbers, and let. The vector space axioms talk about only two operations: • vector space v • subspaces s of vector space v. The degree of the polynomials could be restricted or unrestricted. 4.1 vector spaces & subspaces. W is closed under scalar multiplication:
Vector Spaces And Subspaces , The Degree Of The Polynomials Could Be Restricted Or Unrestricted.
Vector Spaces And Subspaces , The Intersection Of Two Subspaces Is Also A Subspace ...
Vector Spaces And Subspaces : Vector Spaces And Subspaces - Linear Algebra - Youtube
Vector Spaces And Subspaces . Nevertheless, The Idea Of Subtracting Two Vectors Is Hidden Inside Those Axioms.
Vector Spaces And Subspaces - In This Section We Discuss Subspaces Of.
Vector Spaces And Subspaces . A Set Of Objects (Vectors) And A Field (Scalars) Where The Vector Space Is Over.
Vector Spaces And Subspaces . Subspaces Are Vector Spaces In Their Own Right Contained Within The Vector Space.
Vector Spaces And Subspaces - Testing If A Subset Of Vectors Of A Vector Space Gives A Subspace.
Vector Spaces And Subspaces : The Zero Vector Is Given By The Zero Polynomial.
Vector Spaces And Subspaces . R, R2 , R3, Etc) And We Also Know That They Have Many Properties.
Comments
Post a Comment