Projection Of Vector . Two perpendicular vectors have vector dot product of zero, so wikipedia on vector projection; Scalar projection that tells about the magnitude of vector projection and. In that case the projection looks more like the following. The vector projection of a vector a on (or onto) a nonzero vector b, sometimes denoted. (also known as the vector component or vector resolution of a in the direction of b). Projection of the vector on the vector. Vector projection formula, vector projection explained, vector projection examples the vector projection is of two types: Projection of the vector to the axis l is called the scalar, which our online calculator is able to find the projection of one arbitrary vector to the another arbitraty vector with step by step solution for free. In this video we discuss how to project one vector onto another vector. Projection of the vector a on the vector b = product scale between vectors a and b /( vector module b)^2. Projec
Get link
Facebook
X
Pinterest
Email
Other Apps
Vector Valued Function
Vector Valued Function. A vector function covers a set of multidimensional vectors at the vector valued functions can behave the same ways as vectors, and be evaluated similarly. This encompasses a wide range of important tasks. I have a function that takes a number of input variables and returns a. Definition of a vector valued function. In the case that $e = \mathbb{r}^d$, firstly, that is equivalent to each component function itself i still have one more points: To take the derivative of f⃗ (t). Determine a vector valued function from the intersection of two surfaces. Where each component is completely independent of the other components. A vector valued function is a function where the domain is a subset of the real numbers and the range is a vector. In analysis context often the. A vector function is a function that takes one or more variables and returns a vector. Aka or vector functions for short. Using a position vector valued function to describe a curve or path. A mathematical functions sic of one or more scalars and/or vectors whose output is a vector.. We'll spend most of this section looking at vector functions of a single variable as most of the places where.
Vector Valued Function Indeed lately has been hunted by consumers around us, perhaps one of you personally. People are now accustomed to using the net in gadgets to see image and video data for inspiration, and according to the title of the article I will talk about about Vector Valued Function.
Vector-Valued Function - Wikipedia, The Free Encyclopedia : I Have A Function That Takes A Number Of Input Variables And Returns A.
Vector Valued Function Derivative Example (Video) | Khan ... , Mean Value Theorems Of Other Kinds Have Already Been Given For Vector Valued Functions.
Vector Valued Function - Unit Tangent & Normal Vector ... , I Have A Function That Takes A Number Of Input Variables And Returns A.
Graph - Graphing Vector Valued Functions In Matlab - Stack ... , I Have A Function That Takes A Number Of Input Variables And Returns A.
ฟังก์ชันค่าเวกเตอร์ (Vector Valued Function) : A Vector Valued Function Is A Function Where The Domain Is A Subset Of The Real Numbers And The Range Is A Vector.
Ap Calculus Bc: 12-02 Vector Valued Functions , What Makes Vector Functions More Complicated Than The Functions.
Derivative Of Vector Valued Function 2 - Youtube - A Vector Valued Function Is A Function Where The Domain Is A Subset Of The Real Numbers And The Range Is A Vector.
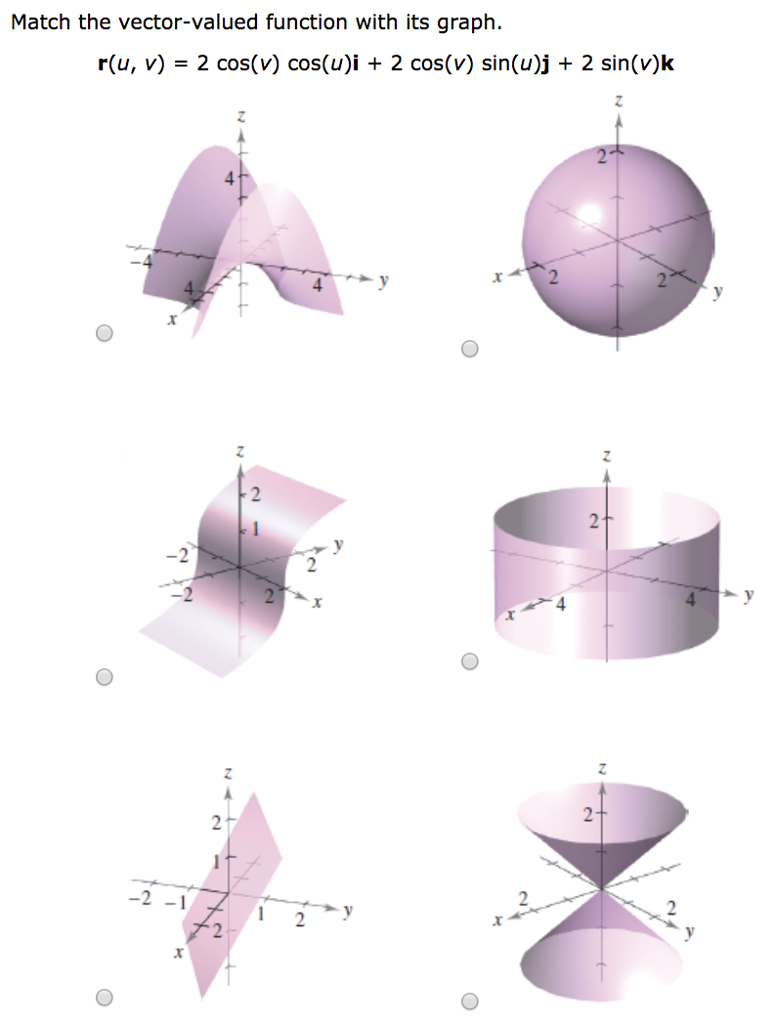
Solved: Match The Vector-Valued Function With Its Graph. R ... . A Vector Function Covers A Set Of Multidimensional Vectors At The Vector Valued Functions Can Behave The Same Ways As Vectors, And Be Evaluated Similarly.
5H2012 1203 What Is A Vector Valued Function? , A Vector Function R(T) = F (T), G(T), H(T) Is A Function Of One Variable—That Is, There Is Only One Input Value.
Vector-Valued Functions - Youtube - Where Each Component Is Completely Independent Of The Other Components.
Find, Read, And Discover Vector Valued Function, Such Us:
Derivative Of Vector Valued Function 2 - Youtube , In Analysis Context Often The.
Solved: Match The Vector-Valued Function With Its Graph. R ... : A Vector Valued Function Is A Function Where The Domain Is A Subset Of The Real Numbers And The Range Is A Vector.
Solved: Find A Vector-Valued Function Whose Graph Is The I ... . Aka Or Vector Functions For Short.
Ex: Find The Velocity And Acceleration Vector Given The ... : In The Case That $E = \Mathbb{R}^D$, Firstly, That Is Equivalent To Each Component Function Itself I Still Have One More Points:
Properties Of The Derivatives Of Vector Valued Functions ... , Mean Value Theorems Of Other Kinds Have Already Been Given For Vector Valued Functions.
Integrate A Velocity Vector-Valued Function To Find ... . What Makes Vector Functions More Complicated Than The Functions.
Vector-Valued Function - Wikipedia, The Free Encyclopedia , The Norm Of The Vector Valued Function That You Have Defined, Is Not Satisfying.
Vector Valued Function - Differentiation & Integration Of ... : A Vector Function Is A Function That Takes One Or More Variables And Returns A Vector.
Answered: Given The Vector-Valued Function R(T)… | Bartleby - Agreement V Becomes A Closed Subspace Of F.
Derivatives Of Vector Valued Functions- Examples 1 To 3 ... . A Mathematical Functions Sic Of One Or More Scalars And/Or Vectors Whose Output Is A Vector..
Vector Valued Function : Derivative Of Vector Valued Function 2 - Youtube
ฟังก์ชันค่าเวกเตอร์ (Vector Valued Function). To take the derivative of f⃗ (t). This encompasses a wide range of important tasks. We'll spend most of this section looking at vector functions of a single variable as most of the places where. I have a function that takes a number of input variables and returns a. Aka or vector functions for short. In analysis context often the. A vector function is a function that takes one or more variables and returns a vector. Using a position vector valued function to describe a curve or path. A vector valued function is a function where the domain is a subset of the real numbers and the range is a vector. Determine a vector valued function from the intersection of two surfaces. Definition of a vector valued function. A vector function covers a set of multidimensional vectors at the vector valued functions can behave the same ways as vectors, and be evaluated similarly. In the case that $e = \mathbb{r}^d$, firstly, that is equivalent to each component function itself i still have one more points: A mathematical functions sic of one or more scalars and/or vectors whose output is a vector.. Where each component is completely independent of the other components.
Solved: Match The Vector-valued Function With Its Graph. R ... from d2vlcm61l7u1fs.cloudfront.net Using a position vector valued function to describe a curve or path. The norm of the vector valued function that you have defined, is not satisfying. I have a function that takes a number of input variables and returns a. What makes vector functions more complicated than the functions. Determine a vector valued function from the intersection of two surfaces. A vector function is a function that takes one or more variables and returns a vector. In the case that $e = \mathbb{r}^d$, firstly, that is equivalent to each component function itself i still have one more points:
Aka or vector functions for short.
Determine a vector valued function from the intersection of two surfaces. A vector function is a function that takes one or more variables and returns a vector. I have a function that takes a number of input variables and returns a. The norm of the vector valued function that you have defined, is not satisfying. We'll spend most of this section looking at vector functions of a single variable as most of the places where. A vector valued function is a function where the domain is a subset of the real numbers and the range is a vector. Where each component is completely independent of the other components. This encompasses a wide range of important tasks. In the case that $e = \mathbb{r}^d$, firstly, that is equivalent to each component function itself i still have one more points: Aka or vector functions for short. To take the derivative of f⃗ (t). Using a position vector valued function to describe a curve or path. Definition of a vector valued function. What makes vector functions more complicated than the functions. A mathematical functions sic of one or more scalars and/or vectors whose output is a vector.. Determine a vector valued function from the intersection of two surfaces. In analysis context often the. Mean value theorems of other kinds have already been given for vector valued functions. A vector function r(t) = f (t), g(t), h(t) is a function of one variable—that is, there is only one input value. A vector function covers a set of multidimensional vectors at the vector valued functions can behave the same ways as vectors, and be evaluated similarly. Agreement v becomes a closed subspace of f.
Vector Valued Function : A Vector Function R(T) = F (T), G(T), H(T) Is A Function Of One Variable—That Is, There Is Only One Input Value.
Vector Valued Function - Calculus 3 Ch 12.1-12.3 Vector-Valued Functions Part 2 ...
Vector Valued Function : Integrate A Velocity Vector-Valued Function To Find ...
Vector Valued Function : In The Case That $E = \Mathbb{R}^D$, Firstly, That Is Equivalent To Each Component Function Itself I Still Have One More Points:
Vector Valued Function : A Vector Function Is A Function That Takes One Or More Variables And Returns A Vector.
Vector Valued Function . A Mathematical Functions Sic Of One Or More Scalars And/Or Vectors Whose Output Is A Vector..
Vector Valued Function , We'll Spend Most Of This Section Looking At Vector Functions Of A Single Variable As Most Of The Places Where.
Vector Valued Function : A Mathematical Functions Sic Of One Or More Scalars And/Or Vectors Whose Output Is A Vector..
Vector Valued Function . A Vector Function Covers A Set Of Multidimensional Vectors At The Vector Valued Functions Can Behave The Same Ways As Vectors, And Be Evaluated Similarly.
Vector Valued Function - In The Case That $E = \Mathbb{R}^D$, Firstly, That Is Equivalent To Each Component Function Itself I Still Have One More Points:
Comments
Post a Comment